
Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác
VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán lớp 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác, bộ tài liệu gồm 10 bài tập trang 40, 41 SGK kèm theo lời giải chi tiết sẽ là nguồn thông tin hữu ích để các bạn học sinh học tập tốt hơn môn Toán.
Giải bài tập Toán 11: Hàm số lượng giác và phương trình lượng giác
Bài 1 trang 40 SGK Đại số 11
a. Hàm số y = cos3x có phải là hàm số chẵn không? Tại sao?
b. Hàm số y = tan(x+ π/5) có phải là hàm số lẻ không? Tại sao?
Lời giải:
a.y= f(x) = cos3x là hàm số chẵn vì:
TXĐ: D = R
∀x∈ D ta có: - x ∈ D
Xét: f(-x) = cos(-3x) = cos3x = f(x)∀ x∈ D
Bài 2 trang 40 SGK Đại số 11
Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x trên đoạn[-3π/2 ; 2π] để hàm số đó:
a. Nhận giá trị bằng -1
b. Nhận giá trị âm
Lời giải:
Đồ thị hàm số y = sinx:
a. Dựa vào đồ thị hàm số, ta thấy trên đoạn [-3π/2; 2π], để hàm số y = sinx nhận giá trị bằng -1 thì x = -/2 và x = 3/2
b. Đồ thị hàm số y = sinx nhận giá trị âm trên đoạn [-3π/2 ; 2π] trong các khoảng (- π, 0) và (π, 2π)
Bài 3 trang 41 SGK Đại số 11
Tìm giá trị lớn nhất của các hàm số sau:
Lời giải:
a. y =
Ta có: cosx ≤ 1
=>1 + cos x ≤ 2 <=> 2(1+cos x) ≤ 4
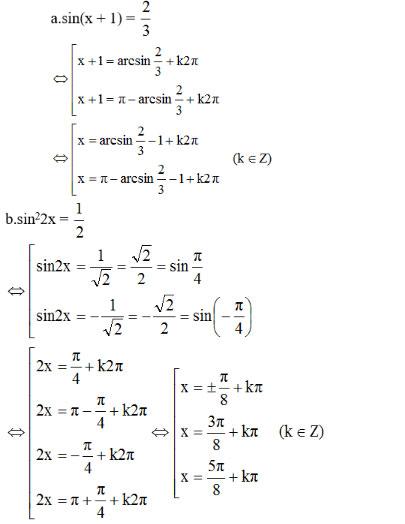
Bài 4 trang 41 SGK Đại số 11
Giải phương trình sau:
Lời giải:
Bài 5 trang 41 SGK Đại số 11
Giải các phương trình sau:
a. 2cos2x - 3cosx + 1 = 0
b. 25sin2x + 15sin2x + 9cos2x = 25
c. 2sinx + cosx = 1
d. sinx + 1,5cotx = 0
Lời giải:
a. 2cos2x - 3cosx + 1 = 0 (1)
Đặt t = cosx với điều kiện - 1 ≤ t ≤ 1
(1) 2t2 - 3t + 1 = 0
b. 25sin2x + 15sin2x + 9cos2x = 25
<=> 25sin2x + 15.2sinx.cosx + 9cos2x = 25(sin2x + cos2x)
<=> 16cos2x - 30sinx.cosx = 0 <=> 2cosx(8cosx - 15sinx) = 0
Điều kiện: sinx ≠ 0 <=> x ≠ kπ (k ∈ Z)
(1)<=> 2sin2x + 3cosx=0 <=>2(1-cos2x) + 3cosx=0
<=>2cos2x - 3cosx - 2 = 0 (2)
Đặt cos x = t với điều kiện - 1 ≤ t ≤ 1
Bài 6 trang 41 SGK Đại số 11
Phương trình cos x = sin x có số nghiệm thuộc đoạn [- π; π] là:
A. 2
B. 4
C. 5
D. 6
Lời giải:
Ta có: sinx = cosx <=> tanx = 1 (cos x ≠ 0 ) <=> x = π/4 + kπ (k ∈ Z)
Họ nghiệm x = π/4 + kπ có hai nghiệm thuộc đoạn [- π; π] tương ứng với k = - 1 và k = 1.
Vậy chọn đáp án A.
Bài 7 trang 41 SGK Đại số 11
Phương trình ...
Lời giải:
(1)<=> cos4x = sin 2x <=>1 - 2sin22x = sin2x
Số nghiệm thuộc khoảng (0; π/2) là hai nghiệm x = π/12 và x = 5π/12
Vậy chọn đáp án A.
Bài 8 trang 41 SGK Đại số 11
Nghiệm dương nhỏ nhất của phương trình sin x + sin 2x = cos x + 2 cos2x là:
Lời giải:
Ta có: sin x + sin2x = cosx + 2cos2x
<=>sin x + 2sinxcosx = cosx(1 + 2cosx)
<=>sinx (1+2cosx) = cosx(1 + 2cosx)
Chọn đáp án C.
Bài 9 trang 41 SGK Đại số 11
Nghiệm âm lớn nhất của phương trình 2tan22x + 5 tanx + 3 = 0 là:
Lời giải:
Ta có: 2tan2x + 5 tanx + 3 = 0
Chọn đáp án B.
Bài 10 trang 41 SGK Hình học 11
Phương trình 2tanx - 2cox - 3 = 0 có số nghiệm thuộc khoảng(-π/2 ; π) là:
A. 1
B. 2
C. 3
D. 4
Lời giải:
2tanx - 2cotx - 3 = 0 (1)
Chọn đáp án C.
Bài tiếp theo: Giải bài tập trang 46 SGK Giải tích 11: Quy tắc đếm
-
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau đồi được nội dung kiến thức của bài viết rồi đúng không ạ? Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 11 nhé. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Hóa học lớp 10, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi thpt Quốc gia môn Văn, Thi thpt Quốc gia môn Lịch sử, Thi thpt Quốc gia môn Địa lý, Thi thpt Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.
Mời bạn đọc cùng tham khảo thêm:
- Giải bài tập trang 28, 29 SGK Giải tích 11: Phương trình lượng giác cơ bản
- Giải bài tập trang 36, 37 SGK Giải tích 11: Một số phương trình lượng giác thường gặp
- Giải bài tập trang 17, 18 SGK Giải tích 11: Hàm số lượng giác
- Đề thi giữa học kì 1 môn Toán lớp 11 trường THPT Giao Thủy, Nam Định
- Đề kiểm tra 45 phút học kì 1 môn Toán lớp 11 trường THPT Phan Ngọc Hiển, Cà Mau
Link nội dung: https://career.edu.vn/on-tap-chuong-1-toan-11-a40819.html