Lý thuyết Ôn tập chương 3 (mới 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Ôn tập chương 3

A. Lý thuyết

1. Hệ tọa độ trong không gian

1.1. Tọa độ của điểm và của vecto

1.1.1. Hệ tọa độ

Trong không gian, xét ba trục tọa độ x’Ox; y’Oy; z’Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi i→;  j→  ;  k→ lần lượt là các vectơ đơn vị, trên các trục x’Ox; y’Oy; z’Oz.

Hệ ba trục như vậy gọi là hệ trục tọa độ Đề- các vuông góc Oxyz trong không gian, hay đơn giản gọi là hệ trục tọa độ Oxyz.

Điểm O được gọi là gốc tọa độ.

Các mặt phẳng (Oxy); (Oyz); (Ozx) đôi một vuong góc với nhau được gọi là các mặt phẳng tọa độ.

Không gian với hệ tọa độ Oxyz còn gọi là không gian Oxyz.

- Vì i→;  j→  ;  k→ là các vecto đơn vị đôi một vuông góc với nhau nên: i→2  =  j→2  =  k→2  =  1 và i→ . j→  =  j→.  k→  =  k→ . i→  =0

1.1.2. Tọa độ của một điểm

- Trong không gian Oxyz, cho một điểm M tùy ý. Vì ba vecto i→;  j→;  k→ không đồng phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho: OM→  = x.i→+ y.  j→ +​z. k→

- Ngược lại, với bộ ba số (x; y; z) ta có một điểm M duy nhất trong không gian thỏa mãn hệ thức OM→  =  x.i→  + y. j→  +​ z.k→

- Ta gọi bộ ba số (x; y; z) là tọa độ của điểm M đối với hệ trục tọa độ Oxyz đã cho và viết: M = ( x; y; z) hoặc M (x; y; z).

1.1.3. Tọa độ của vecto

- Trong không gian Oxyz cho vecto a→, khi đó luôn tồn tại duy nhất bộ ba số (a1; a2; a3) sao cho a→  =  a1.i→  + a2. j→  +​ a3. k→

Ta gọi bộ ba số (a1; a2 ; a3) là tọa độ của vecto a→ đối với hệ tọa độ Oxyz cho trước và viết a→(a1; a2 ; a3) hoặc a→(a1; a2 ; a3).

- Nhận xét : Trong hệ tọa độ Oxyz, tọa độ của điểm M chính là tọa độ của vecto OM→

Ta có: M(x; y; z)⇔OM→  (x; y;  z)

1.2. Biểu thức tọa độ của các phép toán của vecto

- Định lí: Trong không gian Oxyz, cho hai vecto

Ví dụ 1.

Lời giải:

- Hệ quả:

a) Cho hai vecto a→=(a1;a2;a3),  b→=(b1;b2; b3), ta có:

a→=b→  ⇔  a1=b1a2=b2a3=b3

b) Vecto 0→ có tọa độ ( 0; 0; 0).

c) Với b→  ≠0→  thì hai vecto a→;  b→ cùng phương khi và chỉ khi tồn tại số k sao cho:

⇔a→=kb→   (k∈ℝ)

⇔  a1=kb1a2=kb2a3=kb3 ⇔a1b1=a2b2=a3b3,(b1,  b2,  b3≠0)

Ví dụ 2. Cho u→  (2m; 3;  −1);  v→ (4;  3; n−2). Tìm m và n để u→  =  v→ 

Lời giải:

Ví dụ 3. Các cặp vecto sau có cùng phương không?

Lời giải:

a) Ta thấy 2−4  =  3−6  ≠714

Do đó, hai vecto trên không cùng phương.

b) Ta thấy: b→  =  −3a→ nên hai vecto trên cùng phương.

Ví dụ 4. Cho hai điểm A( - 3; 4; 0) và B( -1; 0; 8).

a) Tính AB→ ;

b) Tìm tọa độ trung điểm M của AB.

Lời giải:

1.3. Tích vô hướng.

1.3.1. Biểu thức tọa độ của tích vô hướng.

- Định lí:

Trong không gian Oxyz, tích vô hướng của hai vecto a→=(a1;a2;a3),  b→=(b1;b2; b3)được xác định bởi công thức: a→.b→=a1.b1+a2.b2+a3.b3

Ví dụ 5. Cho a→ (1;−3;4);  b→  (1;2;1). Tính a→. b→ ?

Lời giải:

Ta có: a→. b→ = 1.1 + ( -3). 2 + 4.1 = -1

1.3.2. Ứng dụng

a) Độ dài của một vecto.

b) Khoảng cách giữa hai điểm.

Trong khong gian Oxyz, cho hai điểm A(xA ; yA ; zA)

và B(xB; yB ; zB). Khi đó, khoảng cách giữa hai điểm A và B chính là độ dài của vecto AB→. Do đó, ta có:

c) Góc giữa hai vecto.

Nếu là góc góc giữa hai vecto a→  =  (a1; a2; a3) và b→  =  (b1; b2; b3) với a→;  b→  ≠0→ thì

Từ đó, suy ra a→⊥b→   ⇔  a1b1+a2b2+a3b3=0

Ví dụ 6. Cho tam giác ABC có A(2; 3; 1); B( 2; 1; 0); C( 0; -1; 2).

a) Tính AB; AC

b) Tính cosin của góc A.

Lời giải:

1.4. Phương trình mặt cầu

- Định lí.

Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c) bán kính r có phương trình là:

( x - a)2 + (y - b)2 + (z - c)2 = r2

- Nhận xét. Phương trình mặt cầu nói trên có thể viết dưới dạng:

x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 với d = a2 + b2 + c2 - r2

Từ đó, ta chứng minh được rằng phương trình dạng:

x2 + y2 + z2 + 2Ax + 2By + 2Cz + D = 0 với điều kiện A2 + B2 + C2 - D > 0 là

phương trình mặt cầu có tâm I( -A; -B; - C) có bán kính r=  A2  +  B2+​ C2−​D

Ví dụ 7. Tìm tâm và bán kính của mặt cầu có phương trình sau đây:

a) x2 + y2 + z2 - 4x + 2y - 1 = 0;

b) x2 + y2 + z2 - 8x - 2y + 2z + 2 = 0

Lời giải:

2. Phương trình mặt phẳng

2.1. Vecto pháp tuyến của mặt phẳng.

2.1.1. Định nghĩa:

Cho mặt phẳng (α). Nếu vecto n→  ≠0→ và có giá vuông góc với mặt phẳng (α) thì được n→  gọi là vecto pháp tuyến của (α)

2.1.2. Chú ý. Nếu n→  là vecto pháp tuyến của một mặt phẳng thì kn→  (k ≠0) cũng là vecto pháp tuyến của mặt phẳng đó.

2.1.3. Tích có hướng của hai vectơ

- Định nghĩa: Trong không gian Oxyz, cho hai vectơ a→=(a1;a2;a3), b→=(b1; b2; b3). Tích có hướng của hai vectơ a→ và b→ kí hiệu là a→,b→, được xác định bởi

- Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

Ví dụ 8. Trong không gian Oxyz, cho ba điểm A(2; 1;1); B(-1; 2; 0) và C(0; 1; -2).

Hãy tìm tọa độ của một vecto pháp tuyến của mặt phẳng (ABC).

Lời giải:

2.2. Phương trình tổng quát của mặt phẳng

2.2.1. Định nghĩa.

- Phương trình có dạng Ax + By + Cz + D = 0 trong đó A; B; C không đồng thời bằng 0 , được gọi là phương trình tổng quát của mặt phẳng.

- Nhận xét.

a) Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một vecto pháp tuyến là n→  ( A; B; C).

b) Phương trình mặt phẳng đi qua điểm M (x0; y0; z0) và nhận vectơ n→  ( A; B; C) khác 0→ là vecto pháp tuyến là: A(x- x0 ) + B( y - y0) + C(z - z0) = 0.

Ví dụ 9. Mặt phẳng 2x - y + 3z - 10 = 0 có một vecto pháp tuyến là n→(2; -1; 3).

Ví dụ 10. Lập phương trình tổng quát của mặt phẳng (ABC) với A(0; 1; -2); B(2; 1; 0); C ( -2; 1; 1)

Lời giải:

2.2.2. Các trường hợp riêng

Trong không gian Oxyz, cho mặt phẳng (α) : Ax + By + Cz + D = 0.

a) Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.

b)

- Nếu A=0,B≠0,C≠0 thì mặt phẳng (α) song song hoặc chứa trục Ox.

- Nếu A≠0,B=0,C≠0 thì mặt phẳng (α) song song hoặc chứa trục Oy.

- Nếu A≠0,B≠0,C=0 thì mặt phẳng (α) song song hoặc chứa trục Oz.

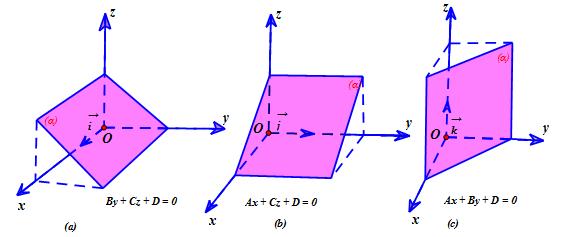
c)

- Nếu A = B = 0; C ≠0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).

- Nếu A = C = 0; B ≠0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).

- Nếu B = C = 0; A ≠0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).

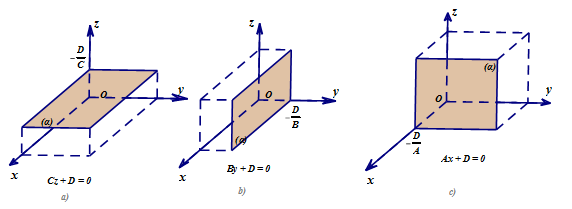
- Nhận xét:

Phương trình mặt phẳng theo đoạn chắn α:xa+yb+zc=1. Ở đây (α) cắt các trục tọa độ tại các điểm (a; 0; 0); (0; b; 0); (0; 0; c) với abc≠0.

Ví dụ 11. Trong không gian Oxyz, cho ba điểm M(2; 0; 0); N(0; 3; 0); P(0; 0; 1). Phương trình đoạn chắn của mp(MNP) là: x2  +​  y3  +​  z1  =1

2.3. Điều kiện để hai mặt phẳng song song, vuông góc.

Trong không gian Oxyz, cho hai mặt phẳng (α) và (β) có phương trình:

(α): A1x + B1y + C1z + D1 = 0

(β): A2x + B2y + C2z + D2 = 0

Hai mặt phẳng (α); (β) có hai vecto pháp tuyến lần lượt là: n1→  (A;1  B1; C1);   n2→  (A;2  B2; C2) 

2.3.1. Điều kiện để hai mặt phẳng song song.

- Chú ý: Để (α) cắt (β)⇔n1→  ≠ k.n2→⇔(A1; B1;C1)≠k(A2;  B2;​​C2)

Ví dụ 12. Viết phương trình mặt phẳng (α) đi qua A(2; 1; 2) và song song với mặt phẳng (P): x - y + 2z - 1 = 0.

Lời giải:

Vì mp(α) song song với mặt phẳng (P): x - y + 2z - 1 = 0 nên nα→ =(1;−1;2)

Mặt phẳng (α) đi qua A(2;1; 2) nên có phương trình:

1( x - 2) - 1(y - 1) + 2( z - 2) = 0 hay x - y + 2z - 5 = 0.

2.3.2. Điều kiện để hai mặt phẳng vuông góc.

(α)  ⊥  (β)  ⇔n1→  ⊥n2→⇔A1A2+​  B1B2+​  C1C2  =0

Ví dụ 13. Viết phương trình mặt phẳng (P) đi qua A(1; 0; 1); B( 2; 1; -1) và vuông góc với mặt phẳng (Q): x - y + 2z - 1 = 0

Lời giải:

Ta có vecto pháp tuyến của mặt phẳng (Q) là:

2.4. Khoảng cách từ một điểm đến một mặt phẳng.

- Định lí: Trong không gian Oxyz, cho điểm M0(x0; y0; z0) và mặt phẳng (α): Ax + By + Cz + D = 0 .

Khi đó khoảng cách từ điểm M0 đến mặt phẳng (α) được tính:

Ví dụ 14. Tính khoảng cách từ điểm M(2; 3; 0) và N( 1; 1; 1) đến mặt phẳng (P): 2x - y + 2z + 1 = 0.

Lời giải:

Theo công thức tính khoảng cách từ một điểm đến mặt phẳng ta có:

Ví dụ 15. Tính khoảng cách giữa hai mặt phẳng song song được cho bởi phương trình: (P): x - 2y +2z + 3 = 0 và (Q): x - 2y + 2z - 7= 0.

Lời giải:

Ta biết khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.

Lấy điểm A(-3; 0; 0) thuộc mặt phẳng (P).

Ta có: d((P); (Q))=d(A;(Q))=−3−2.0+​2.0 −712+​(−2)2+ 22=103

3. Phương trình đường thẳng trong không gian.

3.1. Phương trình tham số của đường thẳng

- Định lí:

Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm M0 (x0 ; y0; z0) và nhận vectơ a →=a1;a2;a3 làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M(x; y; z) nằm trên đường thẳng ∆ là có số thực t thỏa mãn: x=x0+a1ty=y0+a2tz=z0+a2t

- Định nghĩa:

Phương trình tham số của đường thẳng ∆ đi qua điểm M0 (x0 ; y0; z0) và nhận vectơ a →=a1;a2;a3 làm vectơ chỉ phương là x=x0+a1ty=y0+a2tz=z0+a2t

Trong đó, t là tham số.

- Chú ý:

Nếu a1 ; a2; a3 đều khác 0 thì ta có thể viết phương trình ∆ dưới dạng chính tắc như sau:

x−x0a1=y−y0a2=z−z0a3

Ví dụ 16. Viết phương trình tham số của đường thẳng ∆ đi qua A(1; 2;2) và có vecto chỉ phương là u→ (1;2;−1)

Lời giải:

Phương trình tham số của ∆ là: x=  1+​ty=2 +​2tz= 2 −t

Ví dụ 17. Viết phương trình tham số của đường thẳng AB với A(0;1; 2); B(2; 2; 1).

Lời giải:

Đường thẳng AB nhận AB→  (2;1;−1) làm vecto chỉ phương.

Phương trình tham số của AB là: x=  2​ty=1+​tz= 2 −t

3.2. Điều kiện để hai đường thẳng song song, cắt nhau và chéo nhau.

3.2.1. Điều kiện để hai đường thẳng song song.

Gọi a→  = (a1;  a2; a3);a'→  = (a'1;  a'2; a'3) lần lượt là vecto chỉ phương của d và d’.

Lấy điểm M(x0; y0; z0) trên d.

Ta có: d song song với d’ khi và chỉ khi a→ =  k.a'→M  ∉d'

Đặc biệt: d trùng với d’ khi và chỉ khi: a→ =  k.a'→M  ∈d'

Ví dụ 18. Chứng minh hai đường thẳng sau đây song song với nhau:

d:x=  3+​2ty= 2−3tz=  2+t;  d':x=  1−​4ty=  2+​6tz=  −2t

Lời giải:

Đường thẳng d có vecto chỉ phương u→ (2;−3;1) đi qua M(3; 2; 2).

Đường thẳng d’ có vecto chỉ phương là v→ (−4;  6;−2)

Ta thấy: v→  =−2u→;  M∉d'

Do đó, hai đường thẳng trên song song với nhau.

3.2.2. Điều kiện để hai đường thẳng cắt nhau.

- Hai đường thẳng d và d’ cắt nhau khi và chỉ khi hệ phương trình ẩn t và t’ sau:

x0+​ ta1= x'0+​ t'.a'1 y0+​ ta2= y'0+​ t'.a'2 z0+​ ta3= z'0+​ t'.a'3 (I)

Có đúng một nghiệm.

- Chú ý: Giả sử hệ (I) có nghiệm (t0 ; t’0), để tìm giao điểm M0 của d và d’ ta có thể thay t0 vào phương trình tham số của d hoặc thay t’0 vào phương trình tham số của d’.

Ví dụ 19. Tìm giao điểm của hai đường thẳng:

d:  x=  3+​ty= 2−tz=  2+t;  d':  x=  3−​t'y=  2+t'z=  3

Lời giải:

Xét hệ phương trình:

3+ t=3−t'2−t=2+​ t'2+​t  =3 ⇔t=−t't=−t't=1  ⇔t=1;  t'=−1

Suy ra, d cắt d’ tại điểm A(4; 1; 3).

3.2.3. Điều kiện để hai đường thẳng chéo nhau.

Hai đường thẳng d và d’ chéo nhau khi và chỉ khi a→;  a'→ không cùng phương và hệ phương trình x0+​ ta1= x'0+​ t'.a'1 y0+​ ta2= y'0+​ t'.a'2 z0+​ ta3= z'0+​ t'.a'3  vô nghiệm.

Ví dụ 20. Xét vị trí tương đối của hai đường thẳng:

d:  x=  3+​ty= 2−3tz=  2+t;  d':  x=  1−​4t'y=  2+​6t'z=  −2t'

Lời giải:

Đường thẳng d có vecto chỉ phương a→ (1;−3;1)

Đường thẳng d’ có vecto chỉ phương là a'→ (−4;  6;−2)

Ta thấy, không tồn tại số thực k để a→=k  a'→ nên hai đường thẳng d và d’ cắt nhau hoặc chéo nhau.

Xét hệ phương trình:

3+​ t= 1−4t'  (1)2−3t  =2+ 6t'  (2)2+ t  =  −2t'  (3)(I)

Giải hệ phương trình (1) và (2) ta được: t =2; t’ = -1.

Thay vào (3) ta thấy không thỏa mãn nên hệ phương trình (I) vô nghiệm.

Vậy hai đường thẳng d và d’ chéo nhau.

- Nhận xét:

Trong không gian Oxyz, cho mặt phẳng (P): Ax + By + Cz + D = 0 và đường thẳng d: x=x0+a1ty=y0+a2tz=z0+a2t

Xét phương trình A(x0 + ta1 ) + B(y0 + ta2 ) + C (z0 + ta3 ) + D = 0 ( t là ẩn ) (1)

- Nếu phương trình (1) vô nghiệm thì d và (P) không có điểm chung.

Vậy d// (P).

- Nếu phương trình (1) có đúng một nghiệm t = t0 thì d cắt (P) tại điểm

M(x0 + t0 a1;y0 + t0 a2; z0 + t0 a3).

- Nếu phương trình (1) có vô số nghiệm thì d thuộc (P).

Ví dụ 21. Xét vị trí tương đối của đường thẳng d:x= 1+​2ty=−tz=  −2+  t và mặt phẳng (P): 2x - y - z = 0.

Lời giải:Lấy điểm M(1+ 2t; -t; -2 + t) thuộc đường thẳng d.

Thay tọa độ điểm M vào phương trình (P) ta được:

2(1+ 2t) - (- t) - (-2+ t) = 0

⇔2 + 4t + t + 2 - t = 0

⇔4t + 4 = 0⇔t = - 1.

Suy ra, đường thẳng d cắt mặt phẳng (P) tại M( -1; 1; - 3).

B. Bài tập tự luyện

Các bài tập sau đây đều xét trong không gian Oxyz.

Bài 1.

Lời giải:

Bài 2. Cho tam giác MNP biết M(0; -2; 1); N( -2; 1; 2) và P( -1; -2; 3). Tìm tọa độ trọng tâm G của tam giác

Lời giải:

Bài 3. Cho các vecto a→ (1;2;−3);  b→  ( 2;0;3);  c→  (−1;2;1)

Tính a→. b→;  b→. c→

Lời giải:

a→. b→=  1.2+​  2.0  +​(−3).3= −7 b→. c→  = 2.(−1)+ 0.2+3.1= 1

Bài 4. Tìm tâm và bán kính của mặt cầu có phương trình sau:

a) x2 + y2 + z2 + 6x - 2y + 4z - 3 = 0;

b) 2x2 + 2y2 + 2z2 - 4x - 8y + 12z + 2 = 0.

Lời giải:

Bài 5. Lập phương trình mặt cầu thỏa mãn điều kiện:

a) Đường kính MN trong đó M(2; 2; 2); N ( 4; 4; 0);

b) Tâm I(2; -1; 0) và đi qua A( 2; 3; 0)

Lời giải:

Bài 6. Viết phương trình mặt phẳng (P) biết:

a) Đi qua điểm M(0; 1; 2) và nhận n→(2; 1; 1) làm vecto pháp tuyến.

b) Đi qua ba điểm A(1; 0; 0); B(0; -2: 0) và C (0; 0; - 3).

c) Đi qua ba điểm A(1; 1; 2); B(1; 0; 0) và C(0; 2; 1)

Lời giải:

a) Phương trình tổng quát của mặt phẳng (P) là:

2(x - 0) + 1(y - 1) + 1.(z - 2) = 0 hay 2x + y + z - 3 = 0.

Phương trình tổng quát của mặt phẳng (P) là:

3(x - 1) + 2(y -1) - 1(z - 2) = 0 hay 3x + 2y - z - 3 = 0

Bài 7. Hãy viết phương trình mặt phẳng (P) thỏa mãn:

a) Đi qua M(2; 1; 1) và song song với mặt phẳng (Q): x - 2y + z - 3 = 0

b) Đi qua A(1; 2; 0); B( 0; -2; 1) và vuông góc với mặt phẳng (Q); 2x + z - 3 = 0.

Lời giải:

a) Vì mặt phẳng (P) song song với mặt phẳng (Q) nên một vecto pháp tuyến của mặt phẳng (P) là: nP→  =( 1;−2;1)

Phương trình tổng quát của mặt phẳng (P) là:

1( x - 2) - 2(y - 1) + 1(z - 1) = 0 hay x - 2y + z - 1 = 0.

Phương trình tổng quát của mặt phẳng (P) là:

4( x - 1) - 3( y -2) - 8(z - 0) = 0 hay 4x - 3y - 8z + 2 = 0.

Bài 8. Tính khoảng cách từ điểm M(-3; 2; 1) đến mỗi mặt phẳng sau:

a) Mặt phẳng (P): 2x + 2y - 3z - 1 = 0;

b) Mặt phẳng (Q): x + z - 4 = 0

c) Mặt phẳng (H): x - 6 = 0.

Lời giải:

Áp dụng công thức tính khoảng cách từ một điểm đến mặt phẳng ta được:

Bài 9. Viết phương trình tham số của đường thẳng d trong mỗi trường hợp:

a) Đi qua hai điểm A( -2; 0; 1) và B(1; 1; 1).

b) Đi qua A( -2; 1; 1) và song song với đường thẳng x= 1+​2ty=−tz=  −2+  t

c) Đi qua M(0; -2; 1) và vuông góc với mặt phẳng (P): x + 2y - z + 3 = 0.

Lời giải:

a) Đường thẳng AB đi qua điểm A(-2; 0; 1) và nhận vecto AB→ (3;  1;  0) làm vecto chỉ phương nên có phương trình: x= −2+​3ty=tz=  1​

b) Đường thẳng đã cho có vecto chỉ phương là a→ (2 ; −1; 1).

Vì đường thẳng d cần tìm song song với đường thẳng đã cho nên vecto chỉ phương của d là a→ (2 ; −1; 1)

Phương trình tham số của d là   x= −2+​2ty=1−​tz=  1​  +​  t

c) Mặt phẳng (P) có vecto pháp tuyến là: n→​(1;2;−1)

Vì d vuông góc với (P) nên vecto chỉ phương của d là n→​(1;2;−1)

Phương trình tham số của d là x = ty=−2+ 2​tz=  1​  −  t

Bài 10. Xét vị trí tương đối của hai đường thẳng sau:

Lời giải:

a) Đường thẳng d và d’ có vecto chỉ phương lần lượt là: a→ ( 2;  −1;  1)  ;  a'→  ( 1;1;1)

Không tồn tại số thực k để a→  =  k. a'→ nên hai đường thẳng trên sẽ cắt nhau hoặc chéo nhau.

Xét hệ phương trình: −2+​2t=2+​t'  (1)1−​t=t'   (2)  1​  +​  t =3+t'  (3)(I)

Giải hệ phương trình (1) và (2) ta được: t= 53;  t'  = −23

Thay vào (3) ta thấy không thỏa mãn nên hệ phương trình (I) vô nghiệm nên hai đường thẳng đã cho chéo nhau.

b) Đường thẳng d và d’ có vecto chỉ phương lần lượt là: a→ ( 2;  −2;  4)  ;  a'→  ( 1;−1;  2)

Đường thẳng d đi qua điểm M(-2; 1;1)

Ta thấy: a→  =  2. a'→ và điểm M không thuộc đường thẳng d’ nên hai đường thẳng trên song song với nhau.

Bài 11. Tìm số điểm chung của đường thẳng d và mặt phẳng (P) biết:

Lời giải:

Trắc nghiệm Toán 12 Bài: Ôn tập Chương 3 - Phương pháp tọa độ trong không gian

Câu 1. Cho điểm G(1;1;2) là trọng tâm tam giác ABC với A2;1;3,B2;2;1. Chọn kết luận đúng về điểm C.

A. C∈Oy

B. C∈Oxz

C. C∈Oz

D. C∈Oyz

Câu 2. Trong không gian với hệ tọa độ O;i→;j→;k→, cho hai vec tơ a→=2;−1;4,b→=i→−3k→.Tính

A. a→.b→=−11

B. a→.b→=−13

C. a→.b→=5

D. a→.b→=−10

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:x=1y=2+3tz=5−tt∈R. Véc tơ nào dưới đây là vec tơ chỉ phương của d?

A. u1→=0;3;−1

B. u2→=1;3;−1

C. u3→=1;−3;−1

D. u4→=1;2;5

Câu 4. Cho hai vec tơ u→−2;3;1 và v→=1;1;1. Khi đó số thực m=u→.v→ thỏa mãn:

A. m=0

B. m∈0;2

C. m∈−2;0

D. m∈1;3

Câu 5. Trong không gian Oxyz, cho điểm M thỏa mãn hệ thức OM→=2i→+j→. Tọa độ điểm M là:

A. M1;2;0

B. M2;1;0

C. M2;0;1

D. M0;2;1

Câu 6. Hình chiếu của điểm M1;−1;0 lên trục Oz là:

A. N−1;−1;0

B. N1;−1;0

C. N−1;1;0

D. N0;0;0

Câu 7. Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A1;3;−2 và song song với mặt phẳng P:2x−y+3z+4=0 là:

A. 2x−y+3z+7=0

B. 2x+y−3z+7=0

C. 2x+y+3z+7=0

D. 2x−y+3z−7=0

Câu 8. Trong không gian với hệ tọa độ Oxyz, đường thẳng Δ:x1=y1=z2 vuông góc với mặt phẳng nào trong các mặt phẳng sau?

A. P:x+y+z=0

B. β:x+y−z=0

C. α:x+y+2z=0

D. Q:x+y−2z=0

Câu 9. Trong không gian với hệ tọa Oxyz, cho điểm A2;−3;5. Tọa độ điểm A’ là đối xứng của điểm A qua trục Oz là:

A. 2;3;5

B. 2;−3;−5

C. −2;3;5

D. −2;−3;5

Câu 10. Điểm M∈Oxy thì tọa độ điểm M là:

A. Mx;y;0

B. M0;x;y

C. M0;0;z

D. M0;0;1

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Mặt cầu

Lý thuyết Ôn tập chương 2

Lý thuyết Hệ tọa độ trong không gian

Lý thuyết Phương trình mặt phẳng

Lý thuyết Phương trình đường thẳng trong không gian