Hình bình hành lớp 8 |Toán 8 chương trình mới

1. Khái niệm hình bình hành

- Hình bình hành là tứ giác có hai cặp cạnh đối song song.

Tứ giác ABCD là hình bình hành vì AB // DC, AD // BC.

2. Tính chất hình bình hành

- Trong hình bình hành có:

+ Các cạnh đối bằng nhau;

+ Các góc đối bằng nhau;

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

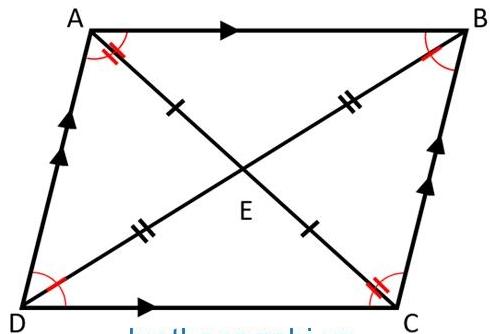
Hình bình hành ABCD có:

+ AB = DC ; AD = BC

+ ;

+ AE = EC ; DE = EB.

3. Dấu hiệu nhận biết hình bình hành

- Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

- Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

>> Xem thêm: Tổng hợp kiến thức toán 8 chi tiết SGK mới

4. Bài tập hình bình hành lớp 8 chương trình mới

4.1 Bài tập hình bình hành sách toán 8 kết nối tri thức

Bài 3.13 trang 61 SGK Toán 8/1 kết nối tri thức

a. Khẳng định đúng: Hình thang là tứ giác có một cặp cạnh song song => hình thang có 2 cạnh bên song song chính là hình bình hành.

b. Khẳng sịnh sai: Hình thang có 2 cạnh bên bằng nhau nhưng không song song không phải là hình bình hành.

c. Khẳng định đúng: Tứ giác có 2 cạnh đối song song là hình bình hành.

Bài 3.14 trang 61 SGK Toán 8/1 kết nối tri thức

Vì ABCD là hình bình hành nên = 100°.

Theo định lí tổng các góc của một tứ giác: large widehat{A}+widehat{B+}widehat{C}+widehat{D}=360^{o}

large Rightarrow 100^{o}+2widehat{B}+100^{o}=360^{o}

large Rightarrow 2widehat{B}=160^{o}Rightarrow widehat{B}=80^{o}

Vậy các góc còn lại của hình bình hành ABCD là

Bài 3.15 trang 61 SGK Toán 8/1 kết nối tri thức

Vì ABCD là hình bình hành nên AB = CD, AB // CD.

Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE = 1/2AB, CF = DF = 1/2CD.

Do đó AE = BE = CF = DF.

Xét tứ giác BEDF có:

BE = DF (chứng minh trên);

BE // DF (vì AB // CD)

Do đó tứ giác BEDF là hình bình hành.

=> BF = DE (đpcm).

Bài 3.16 trang 61 SGK Toán 8/1 kết nối tri thức

a. Hình a

Xét tứ giác ABCD có

Vậy => Tứ giác ABCD là hình bình hành.

b. Hình b

Xét tứ giác ABCD có

Vậy => Tứ giác ABCD không phải là hình bình hành.

c. Hình c

Xét tứ giác ABCD có

Vậy => Tứ giác ABCD là hình bình hành.

Bài 3.17 trang 61 SGK Toán 8/1 kết nối tri thức

a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.

Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE = 1/2AB, CF = DF = 1/2CD

Do đó AE = BE = CF = DF.

• Xét tứ giác AEFD có:

AE // DF (vì AB // CD);

AE = DF (chứng minh trên)

Do đó tứ giác AEFD là hình bình hành.

• Xét tứ giác AECF có:

AE // CF (vì AB // CD);

AE = CF (chứng minh trên)

Do đó tứ giác AECF là hình bình hành.

Vậy hai tứ giác AEFD, AECF là những hình bình hành.

b) Vì tứ giác AEFD là hình bình hành nên EF = AD.

Vì tứ giác AECF là hình bình hành nên AF = EC.

Vậy EF = AD, AF = EC.

Bài 3.18 trang 61 SGK Toán 8/1 kết nối tri thức

Vì ABCD là hình bình hành nên ta có:

• Hai đường chéo AC và BD cắt nhau tại O nên OA = OC, OB = OD.

• AB // CD nên AM // CN suy ra (hai góc so le trong).

Xét ∆OAM và ∆OCN có: (chứng minh trên)

OA = OC (chứng minh trên) (hai góc đối đỉnh)

Do đó ∆ OAM = ∆ OCN (g.c.g).

=> AM = CN (hai cạnh tương ứng)

Mặt khác, AB = CD (chứng minh trên); AB = AM + BM; CD = CN + DN.

Suy ra BM = DN.

Xét tứ giác MBND có:

• BM // DN (vì AB // CD)

• BM = DN (chứng minh trên)

=> tứ giác MBND là hình bình hành.

4.2 Bài tập hình bình hành sách toán 8 chân trời sáng tạo

Bài 1 trang 80 SGK Toán 8/1 chân trời sáng tạo

a. Xét tứ giác ABCD có ở vị trí so le trong => AB // DC.

Để tứ giác ABCD là hình hình hành thì có 2 trường hợp sau:

b. Xét tứ giác EFGH có EH = FG.

Để tứ giác EFGH là hình hình hành thì có 2 trường hợp sau:

c. Xét tứ giác QMPN có O là giao điểm của QN và PM, QO = QN

Để tứ giác QMPN là hình bình hành thì hai đường chéo của tứ giác phải cắt nhau tại trung điểm của mỗi đường.

=> Điều kiện cần là PO = OM thì QMPN là hình bình hành.

d. Xét tứ giác UVST có hai góc đối

=> Để tứ gaisc UVST là hình bình hành thì cần các cặp cạnh đối bằng nhau. Như vậy cần thêm điều kiện để tứ giác UVST là hình bình hành.

Khóa học DUO cung cấp cho các em nền tảng kiến thức toán vững chắc, bứt phá điểm 9+ trong mọi bài kiểm tra trên lớp.

Bài 2 trang 80 SGK Toán 8/1 chân trời sáng tạo

a) Do ABCD là hình bình hành nên AD // BC và AD = BC.

Do AD // BC nên (so le trong)

Xét DADH và DCBK có:

;

AD = BC (chứng minh trên);

(do ).

Do đó DADH = DCBK (cạnh huyền - góc nhọn).

=> AH = CK (hai cạnh tương ứng).

Ta có AH ⊥ DB và CK ⊥ DB nên AH // CK.

Tứ giác AHCK có AH // CK và AH = CK nên AHCK là hình bình hành (dấu hiệu nhận biết).

b. Do AHCK là hình bình hành => đường chéo AC và HK cắt nhau tại trung điểm I của mỗi đường.

=> AI = IC.

Do ABCD là hình bình hành nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của AC nên I là trung điểm của BD, hay IB = ID.

Bài 3 trang 80 SGK Toán 8/1 chân trời sáng tạo

a) ABCD là hình bình hành nên AD = BC và AD // BC.

Mà E là trung điểm của AD nên AE = ED;

F là trung điểm của BC nên BF = FC.

=> DE = BF.

Xét tứ giác EBFD có DE // BF (do AD // BC) và DE = BF nên là hình bình hành (dấu hiệu nhận biết).

b) Ta có O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD.

Do EBFD là hình bình hành nên hai đường chéo BD và EF cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD nên O là trung điểm của EF.

Vậy ba điểm E, O, F thẳng hàng.

Bài 4 trang 80 SGK Toán 8/1 chân trời sáng tạo

a) Do ABCD là hình bình hành nên AB // CD và .

Vì DE là tia phân giác của góc D nên .

Vì BF là tia phân giác của góc B nên .

Do đó .

Do AB // CD nên (so le trong).

Suy ra

Mà hai góc này ở vị trí so le trong nên DE // BF.

b) Tứ giác DEBF có EB // FD (do AB // CD) và DE // BF nên là hình bình hành (dấu hiệu nhận biết).

Bài 5 trang 80 SGK Toán 8/1 chân trời sáng tạo

a) Do ABCD là hình bình hành nên AB = CD và AB // CD.

Vì I là trung điểm của AB nên AI=IB=1/2AB.

Vì K là trung điểm của CD nên CK=DK=1/2CD.

Do đó AI = CK.

Tứ giác AICK có AI // CK (do AB // CD) và AI = CK nên là hình bình hành (dấu hiệu nhận biết).

Suy ra AK // CI hay AE // IF.

Tứ giác AEFI có AE // IF nên là hình thang.

b) Gọi O là giao điểm của hai đường chéo hình bình hành ABCD.

Do đó O là trung điểm của AC và BD.

Xét DABC có BO, CI là hai đường trung tuyến của tam giác và BO, CI cắt nhau tại F nên F là trọng tâm của DABC.

Chứng minh tương tự đối với DACD ta cũng có E là trọng tâm của DACD.

Lại có O là trung điểm BD nên BO = DO.

Lại có:

Vậy DE = EF = FB.

4.3 Bài tập hình bình hành sách toán 8 cánh diều

Bài 1 trang 107 SGK toán 8/1 cánh diều

a) Xét tứ giác ABCD có:

= 360° (tổng các góc của một tứ giác)

Mà (giả thiết)

= 360°

= 360°

= 360°

=180°.

b) Ta có = 180° (hai góc kề bù)

Mà =180°(câu a)

Mà hai góc trên ở vị trí đồng vị nên AD // BC.

c) Xét tứ giác ABCD có: (giả thiết)

Do đó tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).

Bài 2 trang 108 SGK toán 8/1 cánh diều

• Xét ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G (giả thiết) nên G là trọng tâm của ΔABC.

(tính chất trọng tâm của tam giác) (1)

Mà P là trung điểm của GB (giả thiết) nên:

Q là trung điểm của GC (giả thiết) nên

Từ (1), (2) và (3) => GM = GP và GN = GQ.

• Xét tứ giác PQMN có: GM = GP và GN = GQ (chứng minh trên)

Do đó tứ giác PQMN có hai đường chéo MP và NQ cắt nhau tại trung điểm G của mỗi đường nên là hình bình hành.

Bài 3 trang 108 SGK toán 8/1 cánh diều

a) Vì ABCD là hình bình hành (giả thiết) nên AB = CD (tính chất) (1)

Vì ABMN là hình bình hành (giả thiết) nên AB = MN (tính chất) (2)

Từ (1), (2) suy ra CD = MN.

b) Vì ABCD là hình bình hành (giả thiết) nên (tính chất) (3)

Vì ABMN là hình bình hành (giả thiết) nên (tính chất) (4)

Mà (5)

Từ (3), (4) và (5) =>

Bài 4 trang 108 SGK toán 8/1 cánh diều

Xét tứ giác ABCD có: hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Do đó AB = CD = 100 (m).

Trên đây là những kiến thức về hình bình hành lớp 8 trong chương trình toán 8 kết nối tri thức, chân trời sáng tạo và cánh diều. Bên cạnh đó VUIHOC hướng dẫn các em cách giải các bài tập trong sách giáo khoa. Truy cập vuihoc.vn để cập nhật thêm nhiều kiến thức toán 8 bổ ích nhé các em!

>> Mời bạn tham khảo thêm:

Link nội dung: https://career.edu.vn/toan-8-hinh-binh-hanh-a56701.html