There are two different measuring systems to measure an angle. Radian is a unit of measurement of an angle, where one radian is the angle made at the center of a circle by an arc and length equal to the radius of the circle. The degree is another unit that is for the measurement of an angle. When converted from 1 radian to degrees, we have 1 radian equal to 57.296 degrees. The measure of angles can be converted from radians to degrees using a formula.
To understand this 1 radian to degrees formula and the conversion of 1 radian to degrees, we will understand the meaning of each unit of angle. We will also see the radians to degrees chart in this article.
1. What is 1 Radian to Degrees? 2. 1 Radian to Degrees Formula 3. 1 Radian to Degrees: Measures of Angle 4. How to Convert 1 Radian to Degrees? 5. FAQs on 1 Radian to DegreesThe two units used to measure an angle are radians and degrees. We know that 2π radians equal 360 degrees. We will use the unitary method to determine the value of 1 radian to degrees which is equal to 57.296°. This conversion can be done by following some very basic calculations. Therefore, it is necessary to know the formulas for the conversion of units of angle, that is radians to degrees and degrees to radians.
When we rotate the radius completely around the circle, it completes one rotation. The angle subtended at the center of the circle by the radius after one complete rotation is 2π radians. We will use the fact that 2π radians equal 360 degrees to show the conversion of 1 radian to degrees.
2π radians = 360°
Divide the above equation by 2,
⇒ π radians = 180°
Divide the above equation by π,
⇒ 1 radian = 180°/π
⇒ 1 radian = 57.296°
Hence, 1 radian to degrees measures 57.296°
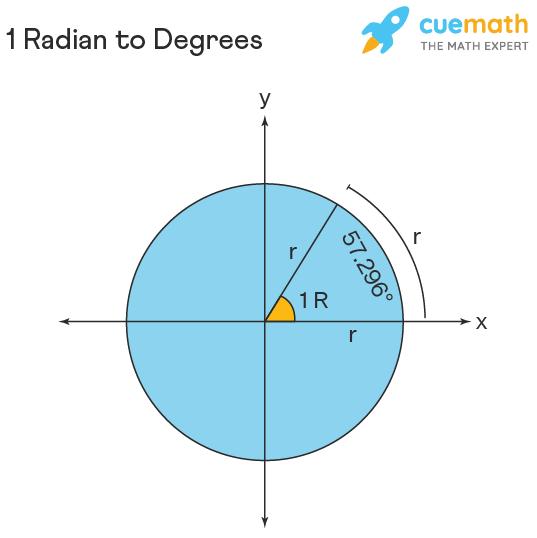
The two units of measurement that are used for measuring angles are degrees and radians. We can convert the measure of any angle from radians to degrees using the conversion of 1 radian to degrees. Let us see what each unit of angle means and how to measure the angle.
Radians
When we rotate the radius completely around the circle, it completes one rotation. The angle subtended at the center of the circle by the radius after one complete rotation is 2π radians. When the length of the arc becomes equal to the length of the radius, the angle subtended at the center becomes 1 radian. We denote the unit radian as rad. Radians is the SI unit of measuring angles.
Degrees
A degree, which is referred to as the degree of arc or arc degree, is the unit of measuring a plane angle. It is denoted by the symbol (°). 360° is the angle measure for a complete rotation. Degrees is not an SI unit to measure angles but it is an accepted unit to measure.
The conversion of radians to degrees can be done using the formula 'Angle in Radians × 180°/π = Angle in Degrees'. We know that 360° equals 2π radians and this result can be used to convert 1 radian to degrees. 360° = 2π radians ⇒ 180° = π radians ⇒ 1 radian = 180°/π ⇒ 1 radian = 57.296°. Using the formula, different angles in radians can be converted to degrees. Let us see the radians to degrees chart where specific angles in radians are given in degrees.

Related Topics to 1 Radian to Degrees
Check out the following pages related to 1 radian to degrees:
- Radians to Degree Calculator
- Degrees to Radians Calculator
- Formula For 180 Degree Rotation
- Radians
- Degrees
Important Notes on 1 Radian to Degrees
Here is a list of a few important points that should be kept in mind while converting 1 radian to degrees :
- 1 radian to degrees measures 57.296° and 1° equals 0.017453 radians.
- The conversion of radians to degrees can be done using the formula 'Angle in Radians × 180°/π = Angle in Degrees'.
- To convert an angle from radians to degrees, we multiply it by 180°/π.
- To convert an angle from degrees to radians, we multiply it by π/180°.



