Đáp án và hướng dẫn giải chi tiết bài tập trong Sách giáo khoa: Bài 34, 35, 36, 37, 38 trang 17 SGK toán 8 tập 1.
Những bài tập này là Bài tập luyện hằng đẳng thức đáng nhớ - chương 1 đại số lớp 8 - Phép nhân và phép chia đa thức.
Bài 34: Rút gọn các biểu thực sau: a) (a + b)2 - (a - b)2; b) (a + b)3 - (a - b)3 - 2b3
c) (x + y + z)2 - 2(x + y + z)(x + y) + (x + y)2
Lời giải: a) (a + b)2 - (a - b)2 = (a2 + 2ab + b2) - (a2 - 2ab + b2)
= a2 + 2ab + b2 - a2 + 2ab - b2 = 4ab
Hoặc (a + b)2 - (a - b)2 = [(a + b) + (a - b)][(a + b) - (a - b)]
= (a + b + a - b)(a + b - a + b)
= 2a . 2b = 4ab
b) (a + b)3 - (a - b)3 - 2b3
= (a3 + 3a2b + 3ab2 + b3) - (a3 - 3a2b + 3ab2 - b3) - 2b3
= a3 + 3a2b + 3ab2 + b3 - a3 + 3a2b - 3ab2 + b3 - 2b3
= 6a2b
Hoặc (a + b)3 - (a - b)3 - 2b3 = [(a + b)3 - (a - b)3] - 2b3
= [(a + b) - (a - b)][(a + b)2 + (a + b)(a - b) + (a - b)2] - 2b3
= (a + b - a + b)(a2 + 2ab + b2 + a2 - b2 + a2 - 2ab + b2) - 2b3
= 2b . (3a2 + b2) - 2b3 = 6a2b + 2b3 - 2b3 = 6a2b
c) (x + y + z)2 - 2(x + y + z)(x + y) + (x + y)2
= x2 + y2 + z2+ 2xy + 2yz + 2xz - 2(x2 + xy + yx + y2 + zx + zy) + x2 + 2xy + y2
= 2x2 + 2y2 + z2 + 4xy + 2yz + 2xz - 2x2 - 4xy - 2y2 - 2xz - 2yz = z2
Bài 35: Tính nhanh: a) 342 + 662 + 68 . 66; b) 742 + 242 - 48 . 74.
Lời giải: a) 342 + 662 + 68 . 66 = 342 + 2 . 34 . 66 + 662 = (34 + 66)2 = 1002 = 10000.
b) 742 + 242 - 48 . 74 = 742 - 2 . 74 . 24 + 242 = (74 - 24)2
=502 =2500
Bài 36: Tính giá trị của biểu thức:
a) x2 + 4x + 4 tại x = 98; b) x3 + 3x2 + 3x + 1 tại x = 99
Lời giải: a) x2 + 4x + 4 = x2 + 2 . x . 2 + 22 = (x+ 2)2
Với x = 98: (98+ 2)2 =1002 = 10000
b) x3 + 3x2 + 3x + 1 = x3 + 3 . 1 . x2 + 3 . x .12+ 13 = (x + 1)3
Với x = 99: (99+ 1)3 = 1003 = 1000000
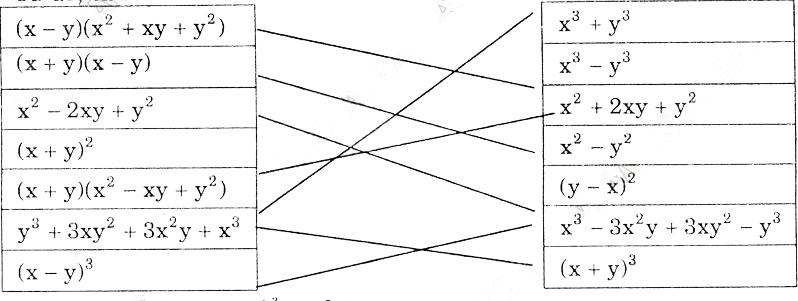
Bài 37:Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu)
(x-y)(x2+xy +y2) x3 + y3 (x+y)(x-y) x3 - y3 x2 - 2xy + y2 x2 + 2xy + y2 (x +y)2 x2 - y2 (x +y)(x2 -xy +2) (y-x)2 y3 + 3xy2 + 3x2y + x3 x3 - 3x2y + 3xy2 - y3 (x-y)3 (x+y)3Ta có: (x - y)(x2 + xy + y2) = X3 - y3 và (x + y)(x2 - xy + y2) = X3 + y3
(x + y) (x - y) = X2 - y2 và X2 - 2xy + y2 = (x - y)2 = (y - x)2 y3 + 3xy2 + 3x2y + X3 = (y + x)3 = (x + y)3 và (x + y)2 = X2 + 2xy + y2 (x - y)3 = X3 - 3x2y + 3xy2 - y3
Từ đó ta có:
Bài 38: Chứng minh các đẳng thức sau:
a) (a - b)3 = -(b - a)3; b) (- a - b)2 = (a + b)2
HD: a) (a - b)3 = -(b - a)3
Biến đổi vế phải thành vế trái:
-(b - a)3= -(b3 - 3b2a + 3ba2 - a3) = - b3 + 3b2a - 3ba2 + a3
= a3 - 3a2b + 3ab2 - b3 = (a - b)3
Sử dụng tính chất hai số đối nhau:
(a - b)3 = [(-1)(b - a)]3 = (-1)3(b - a)3 = -13 . (b - a)3 = - (b - a)3
b) (- a - b)2 = (a + b)2
Biến đổi vế trái thành vế phải:
(- a - b)2 = [(-a) + (-b)]2
= (-a)2 +2 . (-a) . (-b) + (-b)2
= a2 + 2ab + b2 = (a + b)2
Sử dụng tính chất hai số đối nhau:
(-a - b)2 = [(-1) . (a + b)]2 = (-1)2 . (a + b)2 = 1 . (a + b)2 = (a + b)2



