Bài 51 trang 24 SGK Toán lớp 8 tập 1
Câu hỏi:
a.({x^3}-{rm{ }}2{x^2} + {rm{ }}x);
b.(2{x^2} + {rm{ }}4x{rm{ }} + {rm{ }}2{rm{ }}-{rm{ }}2{y^2});
c.(2xy{rm{ }}-{rm{ }}{x^2}-{rm{ }}{y^2} + {rm{ }}16)
Phương pháp:
a.
- Áp dụng các phương pháp phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung, nhóm hạng tử, dùng hằng đẳng thức.
- Áp dụng hằng đẳng thức:
(eqalign{& {left( {A - B} right)^2} = {A^2} -2AB + {B^2} cr} )
b.
- Áp dụng các phương pháp phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung, nhóm hạng tử, dùng hằng đẳng thức.
- Áp dụng các hằng đẳng thức:
(eqalign{& {left( {A + B} right)^2} = {A^2} + 2AB + {B^2} cr & {A^2} - {B^2} = left( {A - B} right)left( {A + B} right) cr} )
c.
- Áp dụng các phương pháp phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung, nhóm hạng tử, dùng hằng đẳng thức.
- Áp dụng các hằng đẳng thức:
(eqalign{& {left( {A - B} right)^2} = {A^2} - 2AB + {B^2} cr & {A^2} - {B^2} = left( {A - B} right)left( {A + B} right) cr} )
Lời giải:
a) x3 - 2x2 + x
= x.x2 - x.2x + x (Xuất hiện nhân tử chung là x)
= x(x2 - 2x + 1) (Xuất hiện hằng đẳng thức (2))
= x(x - 1)2
b) 2x2 + 4x + 2 - 2y2 (có nhân tử chung là 2)
= 2.(x2 + 2x + 1 - y2) (Xuất hiện x2 + 2x + 1 là hằng đẳng thức
= 2[(x2 + 2x + 1) - y2]
= 2[(x + 1)2 - y2] (Xuất hiện hằng đẳng thức (3))
= 2(x + 1 - y)(x + 1 + y)
c) 2xy - x2 - y2 + 16 (Có 2xy ; x2 ; y2, ta liên tưởng đến HĐT (1) hoặc (2))
= 16 - (x2 - 2xy + y2)
= 42 - (x - y)2 (xuất hiện hằng đẳng thức (3))
= [4 - (x - y)][4 + (x - y)]
= (4 - x + y)(4 + x - y).
Bài 52 trang 24 SGK Toán lớp 8 tập 1
Câu hỏi:
Chứng minh rằng ((5n + 2)^2- 4) chia hết cho (5) với mọi số nguyên (n).
Phương pháp:
Áp dụng tính chất chia hết của một tích:
Nếu trong một tích các số nguyên có một thừa số chia hết cho một số nào đó thì tích cũng chia hết cho số đó.
Sử dụng:
({A^2} - {B^2} = left( {A + B} right)left( {A - B} right))
Lời giải:
Ta có:
(5n + 2)2 - 4
= (5n + 2)2 - 22
= (5n + 2 - 2)(5n + 2 + 2)
= 5n(5n + 4)
Vì 5 ⋮ 5 nên 5n(5n + 4) ⋮ 5 ∀n ∈ Ζ.
Vậy (5n + 2)2 - 4 luôn chia hết cho 5 với n ∈ Ζ
Bài 53 trang 24 SGK Toán lớp 8 tập 1
Câu hỏi:
a.(x^2- 3x + 2);
(Gợi ý: Ta không áp dụng ngay các phương pháp đã học để phân tích nhưng nếu tách hạng tử (-3x = - x - 2x) thì ta có (x^2- 3x + 2 = x^2- x - 2x + 2) và từ đó dễ dàng phân tích tiếp.
Cũng có thể tách (2 = - 4 + 6), khi đó ta có (x^2- 3x + 2 = x^2- 4 - 3x + 6), từ đó dễ dàng phân tích tiếp)
b.(x^2+ x - 6);21
c. (x^2+ 5x + 6).
Phương pháp:
a. Áp dụng phương pháp: tách, nhóm, đặt nhân tử chung.
Cách 1: Tách (-3x=-x-2x)
Cách 2: Tách (2=-4+6)
b.
Áp dụng phương pháp: tách, nhóm, đặt nhân tử chung.
Cách 1: Tách (x=3x-2x)
Cách 2:
Thêm bớt để xuất hiện hằng đẳng thức ({left( {A + B} right)^2} = {A^2} + 2AB + {B^2}) và
({A^2} - {B^2} = left( {A + B} right)left( {A - B} right))
c.
Áp dụng phương pháp: tách, nhóm, đặt nhân tử chung.
Cách 1: Tách (5x=2x+3x)
Cách 2:
Thêm bớt để xuất hiện hằng đẳng thức ({left( {A + B} right)^2} = {A^2} + 2AB + {B^2}) và
({A^2} - {B^2} = left( {A + B} right)left( {A - B} right))
Lời giải:
a) Cách 1: x2 - 3x + 2
= x2 - x - 2x + 2 (Tách -3x = - x - 2x)
= (x2 - x) - (2x - 2)
= x(x - 1) - 2(x - 1) (Có x - 1 là nhân tử chung)
= (x - 1)(x - 2)
Cách 2: x2 - 3x + 2
= x2 - 3x - 4 + 6 (Tách 2 = - 4 + 6)
= x2 - 4 - 3x + 6
= (x2 - 22) - 3(x - 2)
= (x - 2)(x + 2) - 3.(x - 2) (Xuất hiện nhân tử chung x - 2)
= (x - 2)(x + 2 - 3)
= (x - 2)(x - 1).
Cách 3: x2 - 3x + 2

b) Cách 1: x2 + x - 6
= x2 + 3x - 2x - 6 (Tách x = 3x - 2x)
= x(x + 3) - 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x - 2)
Cách 2: x2 + x - 6
= x2 + x - 4 - 2 (Tách - 6 = - 4 - 2)
= (x2 - 4) + x - 2
= (x - 2)(x + 2) + (x - 2) (có x - 2 là nhân tử chung)
= (x - 2)[(x + 2) + 1]
= (x - 2)(x + 3)
Cách 3: x2 + x - 6
c) Cách 1: x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: x2 + 5x + 6 (Tách 6 = 10 - 4)
= x2 + 5x + 10 - 4
= (x2 - 4) + (5x + 10) (Có x + 2 là nhân tử chung)
= (x - 2)(x + 2) + 5(x + 2)
= (x + 2)(x + 3)
Cách 3: x2 + 5x + 6
Bài 54 trang 24 SGK Toán lớp 8 tập 1
Câu hỏi:
Phân tích các đa thức sau thành nhân tử:
a.({x^3} + {rm{ }}2{x^2}y{rm{ }} + {rm{ }}x{y^2}-{rm{ }}9x);
b.(2x{rm{ }}-{rm{ }}2y{rm{ }}-{rm{ }}{x^2} + {rm{ }}2xy{rm{ }}-{rm{ }}{y^2});
c.({x^4}-{rm{ }}2{x^2}).
Phương pháp:
c.
- Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm, hằng đẳng thức, đặt nhân tử chung.
- Áp dụng hằng đẳng thức:
(eqalign{ & {A^2} - {B^2} = left( {A - B} right)left( {A + B} right) cr} )
b.
- Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm, hằng đẳng thức, đặt nhân tử chung.
- Áp dụng hằng đẳng thức:
(eqalign{& {left( {A - B} right)^2} = {A^2} - 2AB + {B^2} cr & {A^2} - {B^2} = left( {A - B} right)left( {A + B} right) cr} )
a.
- Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm, hằng đẳng thức, đặt nhân tử chung.
- Áp dụng hằng đẳng thức:
(eqalign{& {left( {A + B} right)^2} = {A^2} + 2AB + {B^2} cr & {A^2} - {B^2} = left( {A - B} right)left( {A + B} right) cr} )
Lời giải:
a) x3 + 2x2y + xy2 - 9x
(Có x là nhân tử chung)
= x(x2 + 2xy + y2 - 9)
(Có x2 + 2xy + y2 là hằng đẳng thức)
= x[(x2 + 2xy + y2) - 9]
= x[(x + y)2 - 32]
(Xuất hiện hằng đẳng thức (3)]
= x(x + y - 3)(x + y + 3)
b) 2x - 2y - x2 + 2xy - y2
(Có x2 ; 2xy ; y2 ta liên tưởng đến HĐT (1) hoặc (2))
= (2x - 2y) - (x2 - 2xy + y2)
= 2(x - y) - (x - y)2
(Có x - y là nhân tử chung)
= (x - y)[2 - (x - y)]
= (x - y)(2 - x + y)
c) x4 - 2x2 (Có x2 là nhân tử chung)
= x2(x2 - 2)
Bài 55 trang 25 SGK Toán lớp 8 tập 1
Câu hỏi:
Lời giải:

b) Ta có: (2x - 1)2 - (x + 3)2 =0 (xuất hiện HĐT (3))
⇔ [(2x - 1) - (x + 3)][(2x - 1) + (x + 3)] = 0
⇔ (2x - 1 - x - 3).(2x - 1 + x + 3) = 0
⇔ (x - 4)(3x + 2) = 0

Bài 56 trang 25 SGK Toán lớp 8 tập 1
Câu hỏi:
Tính nhanh giá trị của đa thức:
(x^2+ dfrac{1}{2}x+ dfrac{1}{16}) tại (x = 49,75);
(x^2- y^2- 2y - 1) tại (x = 93) và (y = 6).
Phương pháp:
Phân tích các đa thức đó thành nhân tử bằng phương pháp dùng hằng đẳng thức rồi thay các giá trị tương ứng của (x, y) để tính giá trị của đa thức đó.
Lời giải:
a) Ta có:
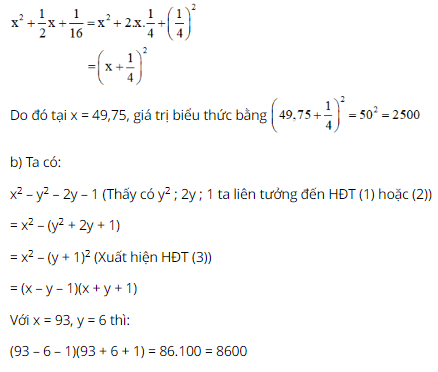
Bài 57 trang 25 SGK Toán lớp 8 tập 1
Câu hỏi:
Phân tích các đa thức sau thành nhân tử:
a.({x^2} - 4x + 3);
b.({x^2} + 5x + 4);
c.({x^2} - x - 6);
d.({x^4} + 4)
Phương pháp:
Áp dụng các phương pháp: nhóm, tách, thêm bớt để xuất hiện nhân tử chung.
Lời giải:
a) Cách 1: x2 - 4x + 3
= x2 - x - 3x + 3
(Tách -4x = -x - 3x)
= x(x - 1) - 3(x - 1)
(Có x - 1 là nhân tử chung)
= (x - 1)(x - 3)
Cách 2: x2 - 4x + 3
= x2 - 2.x.2 + 22 + 3 - 22
(Thêm bớt 22 để có HĐT (2))
= (x - 2)2 - 1
(Xuất hiện HĐT (3))
= (x - 2 - 1)(x - 2 + 1)
= (x - 3)(x - 1)
b) x2 + 5x + 4
= x2 + x + 4x + 4
(Tách 5x = x + 4x)
= x(x + 1) + 4(x + 1)
(có x + 1 là nhân tử chung)
= (x + 1)(x + 4)
c) x2 - x - 6
= x2 + 2x - 3x - 6
(Tách -x = 2x - 3x)
= x(x + 2) - 3(x + 2)
(có x + 2 là nhân tử chung)
= (x - 3)(x + 2)
d) x4 + 4
= (x2)2 + 22
= x4 + 2.x2.2 + 4 - 4x2
(Thêm bớt 2.x2.2 để có HĐT (1))
= (x2 + 2)2 - (2x)2
(Xuất hiện HĐT (3))
= (x2 + 2 - 2x)(x2 + 2 + 2x)
Bài 58 trang 25 SGK Toán lớp 8 tập 1
Câu hỏi:
Chứng minh rằng ({n^3} - n) chia hết cho (6) với mọi số nguyên (n.)
Phương pháp:
Phân tích đa thức đã cho thành nhân tử, sau đó áp dụng tính chất: Một số chia hết cho (2) và (3) thì số đó chia hết cho (6.)
Lời giải:
A = n3 - n (có nhân tử chung n)
= n(n2 - 1) (Xuất hiện HĐT (3))
= n(n - 1)(n + 1)
n - 1; n và n + 1 là ba số tự nhiên liên tiếp nên
+ Trong đó có ít nhất một số chẵn ⇒ (n - 1).n.(n + 1) ⋮ 2
+ Trong đó có ít nhất một số chia hết cho 3 ⇒ (n - 1).n.(n + 1) ⋮ 3
Vậy A ⋮ 2 và A ⋮ 3 nên A ⋮ 6.
Sachbaitap.com



