Giải bài tập Toán 7 Luyện tập chung trang 38
Video giải bài tập Toán 7 Luyện tập chung trang 38
Bài 2.19 trang 38 Toán 7 Tập 1: Cho bốn phân số: 1780;611125;13391 và 98
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết 2=1,414213562..., hãy so sánh phân số tìm được trong câu a) với 2
Lời giải:
a) Bằng cách thực hiện đặt phép tính chia ta có:
1780=0,2125; 611125=4,888; 13391=1,(461538); 98=1,125.
Nhận thấy các số 0,2125; 4,888 và 1,125 là các số thập phân hữu hạn, nên các số 1780;611125 và 98 viết được dưới dạng số thập phân hữu hạn.
Số 1,(461538) là số thập phân vô hạn tuần hoàn với chu kì 461538 nên 13391 không viết được dưới dạng số thập phân hữu hạn.
Vậy 13391 không viết được dưới dạng số thập phân hữu hạn.
b) Số thoả mãn tìm được trong câu a là 13391= 1,(461538) = 1,4615384615…
Theo đề bài 2=1,414213562...
Do 1,4615384615… > 1,414213562… nên 13391>2.
Vậy 13391>2.
Bài 2.20 trang 38 Toán 7 Tập 1:
a) Viết các phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để chỉ rõ chu kì): 19;199.
Em có nhận xét gì về kết quả nhận được?
b) Em hãy dự đoán dạng thập phân của 1999
Lời giải:
a) Bằng cách thực hiện đặt phép tính chia ta có:
19=0,11111...=0,1; 199=0,010101...=0,01.
Nhận xét: Quan sát kết quả của 2 phân số trên, ta thấy số chữ số 0 trong chu kì bằng số chữ số 9 của mẫu số trừ đi 1, sau đó đến một chữ số 1.
b) Phân số 1999 là phân số tối giản có mẫu số là 999 là số có 3 chữ số nên số chữ số 0 có trong chu kì dạng thập phân là 2, sau 2 chữ số 0 này sẽ đến một chữ số 1.
Vậy ta dự đoán dạng thập phân của 1999 là 0,(001).
Bài 2.21 trang 38 Toán 7 Tập 1: Viết 59 và 599 dưới dạng số thập phân vô hạn tuần hoàn.
Lời giải:
Ta sẽ sử dụng kết quả của Bài 2.20 để viết các số 59 và 599 dưới dạng số thập phân vô hạn tuần hoàn như sau:
59=5.19=5.0,1=0,5 và 599=5.199=5.0,01=0,05.
Bài 2.22 trang 38 Toán 7 Tập 1: Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B, C như sau:
a) Hãy cho biết hai điểm A, B biểu diễn những số thập phân nào?
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.
Lời giải:
Quan sát hình trên ta thấy đoạn thẳng đơn vị (từ số 13 đến số 14) được chia làm 2 đoạn bằng nhau, mỗi đoạn này lại được chia thành 5 đoạn bằng nhau, khi đó đoạn thẳng đơn vị cũ được chia thành 10 đoạn đơn vị mới, mỗi đoạn đơn vị mới bằng 110=0,1.
a) Điểm A nằm sau điểm 13 (nằm bên phải điểm 13) và cách điểm 13 một khoảng bằng 4 đoạn 0,1 nên điểm A biểu diễn số 13 + 4.0,1 = 13,4.
Điểm B nằm sau điểm 13 (nằm bên phải điểm 13) và cách điểm 13 một khoảng bằng 12 đoạn 0,1 nên điểm B biểu diễn số 13 + 12.0,1 = 14,2.
Ta cũng có thể tìm số biểu diễn điểm B bằng cách: Quan sát thấy điểm B nằm sau điểm 14 (nằm bên phải điểm 14) và cách điểm 14 một khoảng bằng 2 đoạn 0,1 nên điểm B biểu diễn số 14 + 2.0,1 = 14,2.
b) Giả sử điểm D là điểm nằm sau điểm 14 và cách điểm 14 một khoảng bằng 6 đoạn 0,1 (như hình vẽ) nên điểm D biểu diễn số 14 + 6.0,1 = 14,6.
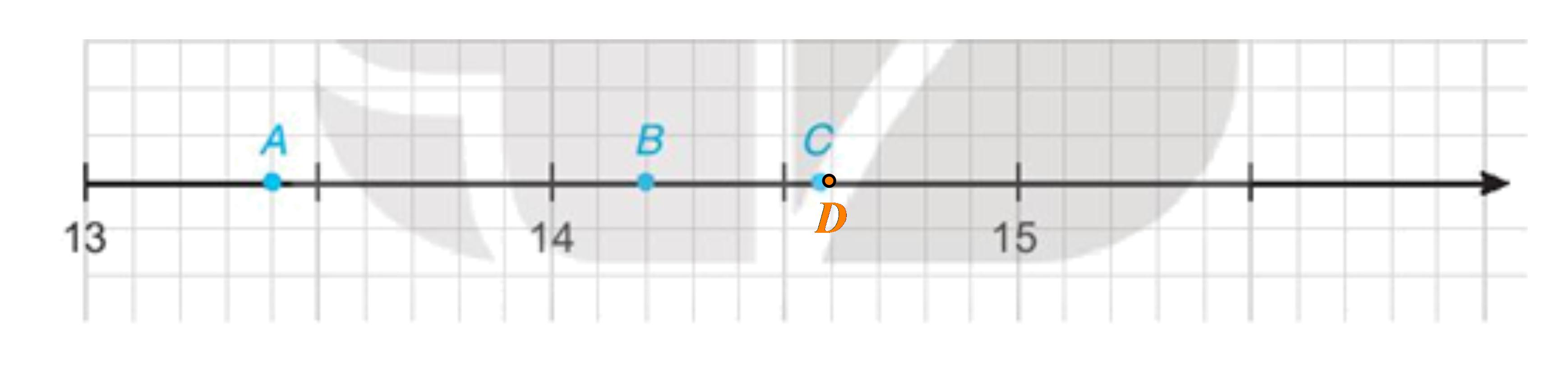
Quan sát hình ta thấy điểm C nằm sau điểm 14 (nằm bên phải điểm 14) và nằm trước điểm D (nằm bên trái điểm D) với khoảng cách rất nhỏ. Do vậy ta làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05 sẽ có kết quả xấp xỉ số thập phân biểu diễn bởi điểm D là 14,6.
Vậy số thập phân được biểu diễn bởi điểm C xấp xỉ bằng 14,6.
Bài 2.23 trang 38 Toán 7 Tập 1: Thay dấu “?” bằng chữ số thích hợp.
a) −7,02<−7,?1;
b) −15,3?021<−15,3819.
Lời giải:
a) Quan sát phần nguyên của hai số thập phân ta thấy chúng đều có phần nguyên bằng -7.
Mà số ở hàng phần trăm của hai số -7,02 và −7,?1 lần lượt là 2 và 1, trong đó 2 > 1 nên để −7,02<−7,?(1) thì số cần điền ở hàng phần mười của số −7,?1 phải là 0.
Khi đó −7,02<−7,0(1).
Vậy ? = 0.
b) Quan sát phần nguyên của hai số thập phân ta thấy chúng đều có phần nguyên bằng -15.
Mà số ở hàng phần mười của hai số −15,3?021 và -15,3819 đều là 3, số ở hàng phần trăm của -15,3819 là 8 nên để −15,3?021<−15,3819 thì số cần điền ở hàng phần trăm của số −15,3?021 phải lớn hơn 8, tức là 9.
Khi đó −15,39021<−15,3819.
Vậy ? = 9.
Bài 2.24 trang 38 Toán 7 Tập 1: So sánh:
a) 12,26 và 12,(24);
b) 31,3(5) và 29,9(8).
Lời giải:
a) Nhận thấy hai số 12,26 và 12,(24) có phần nguyên đều bằng 12 nên ta sẽ so sánh phần thập phân của hai số.
Áp dụng quy tắc làm tròn để làm tròn kết quả với độ chính xác 0,0005 được 12,(24) = 12,242424… ≈ 12,242.
Mà 12,26 > 12,242 nên 12,26 > 12,(24).
Vậy 12,26 > 12,(24).
b) Nhận thấy phần nguyên của hai số 31,3(5) và 29,9(8) lần lượt là 31 và 29 mà 31 > 29 nên 31,3(5) > 29,9(8).
Vậy 31,3(5) > 29,9(8).
Bài 2.25 trang 38 Toán 7 Tập 1: Tính:
a) 1;
b) 1+2+1;
c) 1+2+3+2+1.
Lời giải:
a) Vì 1 = 12 và 1 > 0 nên 1=1.
Vậy 1=1.
b) Ta có 1+2+1=4.
Vì 4 = 22 và 2 > 0 nên 4=2. Do đó 1+2+1=2.
Vậy1+2+1=2.
c) Ta có 1+2+3+2+1=9.
Vì 9 = 32 và 3 > 0 nên 9=3. Do đó 1+2+3+2+1=3.
Vậy 1+2+3+2+1=3.
Bài 2.26 trang 38 Toán 7 Tập 1: Tính:
a) 32;
b) 212.
Lời giải:
a) Ta có 32=3. (theo định nghĩa căn bậc hai số học)
b) Ta có: 212=21. (theo định nghĩa căn bậc hai số học)
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 2 trang 39
Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Luyện tập chung trang 50
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 7. Tập hợp các số thực



